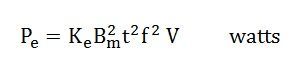When an alternating magnetic field is applied to a magnetic material, an emf is induced in the material itself according to Faraday’s Law of Electromagnetic induction. Since the magnetic material is a conducting material, these EMFs circulate current within the body of the material.
These circulating currents are called Eddy Currents. They will occur when the conductor experiences a changing magnetic field.
As these currents are not responsible for doing any useful work, and it produces a loss (I2R loss) in the magnetic material known as an Eddy Current Loss. Similar to hysteresis loss, eddy current loss also increases the temperature of the magnetic material.
The hysteresis and the eddy current losses in a magnetic material are also known by the name iron losses or core losses or magnetic losses.
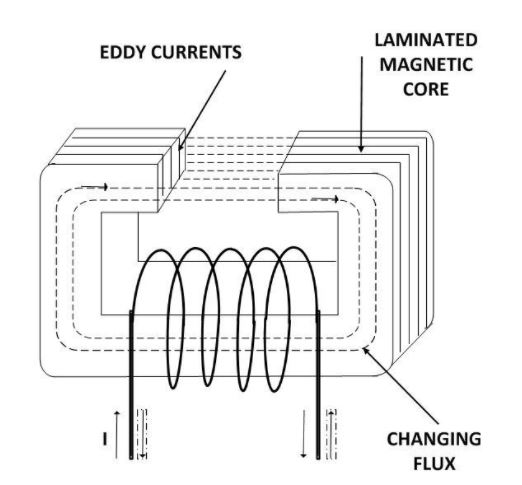
A sectional view of the magnetic core is shown in the figure above. When the changing flux links with the core itself, it induces emf in the core which in turns sets up the circulating current called Eddy Current. And these current in return produces a loss called eddy current loss or (I2R) loss, where I is the value of the current and R is the resistance of the eddy current path.
If the core is made up of solid iron of larger cross-sectional area, the magnitude of I will be very large and hence losses will be high. To reduce the eddy current loss mainly there are two methods.
- By reducing the magnitude of the eddy current.
The magnitude of the current can be reduced by splitting the solid core into thin sheets called laminations, in the plane parallel to the magnetic field. Each lamination is insulated from the other by a thin layer of coating of varnish or oxide film.
By laminating the core, the area of each section is reduced and hence the induced emf also reduces. As the area through which the current is passed is smaller, the resistance of eddy current path increases.
- The eddy current loss is also reduced by using a magnetic material having a higher value of resistivity like silicon steel. Contents:
- Applications of Eddy Currents
- Mathematical Expression for Eddy Current Loss
Applications of Eddy Currents
As you know that by the effect of Eddy Current the heat which is produced is not utilized for any useful work as they are a major source of energy loss in AC machines like transformer, generators, and motors. Therefore, it is known as an Eddy Current Loss. However, there are some uses of this eddy current like in Induction heating.
- In the case of induction heating, an iron shaft is placed as a core of an induction coil. A large amount of heat is produced at the outermost part of the shaft by the eddy current when the high-frequency current is passed through the coil.
At the centre of the shaft, the amount of heat reduces. This is because the outermost periphery of the shaft offers a low resistance path for the eddy currents. This process is used in automobiles for surface hardening of heavy shafts. - The effect of eddy current is also used in electrical instruments like in induction type energy meters for providing braking torque
- For providing damping torque in permanent magnet moving coil instruments.
- Eddy current instruments are used for detecting cracks in metal parts.
- Used in trains having eddy currents brakes.
Mathematical Expression for Eddy Current Loss
It is difficult to determine the eddy current loss from the resistance and current values, but by the experiments, the eddy current power loss in a magnetic material is given by the equation shown below:
where,
Ke – co-efficient of eddy current. Its value depends upon the nature of magnetic material
Bm – maximum value of flux density in wb/m2
T – thickness of lamination in meters
F – frequency of reversal of the magnetic field in Hz
V – volume of magnetic material in m3
This is all about Eddy Current loss.